
АО «НТЦД»
Центр диагностикиE-mail:

Адрес: 109518, г. Москва, ул. Газгольдерная, д. 14, оф. 329
Телефон/Факс: (495) 690-9195


Математические вибрационные модели оборудованияМатематические вибрационные модели внутрикорпусных устройств и топливных сборок реакторов типа ВВЭРСовременные концепции безопасности реакторных установок базируются на широком применении систем оперативной диагностики. В настоящее время одними из наиболее перспективных являются системы вибродиагностики, результатом работы которых является определение и прогнозирования технического состояния оборудования по анализу виброшумовых сигналов. При использовании таких систем возникает проблема интерпретации результатов мониторинга, идентификации аномалий, создания алгоритмов вибродиагностики и экспертных систем. Один из подходов к решению этой проблемы основан на разработке математических моделей динамических процессов. Этот подход позволяет получить динамические характеристики, спектры колебаний и параметры динамического нагружения как для штатного, так и для аномальных состояний оборудования. Перспективность математического моделирования определяется тем, что физическое моделирование на реально действующем оборудовании весьма дорогостояще, а моделирование аномальных состояний практически невозможно. Моделирование гидроупругих систем представляет собой достаточно сложную задачу, поскольку все оборудование взаимосвязано, а в ряде случаев существенным является взаимодействие конструкций с жидкостью. Прямая дискретизация такой системы нецелесообразна, это ведет к модели очень большой размерности, чрезмерно громоздкой для расчетов. Более того, в этом случае трудно интерпретировать результаты расчета, так как они содержали бы большое количество неинформативных характеристик колебаний моделируемой системы. В связи с этим сформулирован и реализован подход к расчетному моделированию сложных систем. В основе его лежит разработка целого спектра моделей различного уровня. Для моделирования используется метод конечных элементов, как наиболее универсальный для сложных пространственных систем. Первым уровнем являются наиболее подробные модели отдельных элементов оборудования (например, корпуса ГЦН и ПГ, опорные конструкции, ТВС и т.д.) как локальных систем (локальные модели). Далее, на основе результатов расчета по локальным моделям разрабатываются упрощенные модели элементов, из которых собирается модель укрупненного фрагмента, подсистемы или всего контура в целом. В качестве упрощенных моделей могут быть применены матрицы жесткости для опорных узлов, стержневые модели или суперэлементы (как в методе подконструкций). Данный подход позволяет анализировать как колебания системы в целом (как правило, низкочастотные), так и детально колебания отдельных элементов в более высокочастотной области спектра. На этапе разработки моделей различного уровня необходимо провести анализ возможных аномалий, для того чтобы была предусмотрена возможность их моделирования. Следующими важными звеньями схемы являются методики расчета собственных характеристик и параметров вынужденных колебаний для моделей оборудования. Результаты этих расчетов составляют базу знаний вибрационных параметров установки. Для расчетов вынужденных колебаний необходима модель вынуждающего воздействия. Для большинства гидромеханических систем основными источниками возбуждения колебаний являются нестационарные гидродинамические процессы в теплоносителе (акустические волны, турбулентность, вихреобразование, кавитация и др.) и несбалансированность вращающихся механизмов, в первую очередь циркуляционных насосов (механические силы). Важным этапом является настройка моделей по экспериментальным данным. Для этого целесообразно использовать специальные алгоритмы, основанные на анализе чувствительности и методиках оптимизации. Данные алгоритмы также целесообразно использовать для диагностики аномалий по результатам измерений. Примером может служить моделирование колебаний внутрикорпусных устройств (ВКУ) реактора ВВЭР-440. Модель реактора выполнена средствами программного комплекса ANSYS. При построении модели использованы трубчатые конечные элементы, для которых задаются:
Из трубчатых конечных элементов составляются модели:
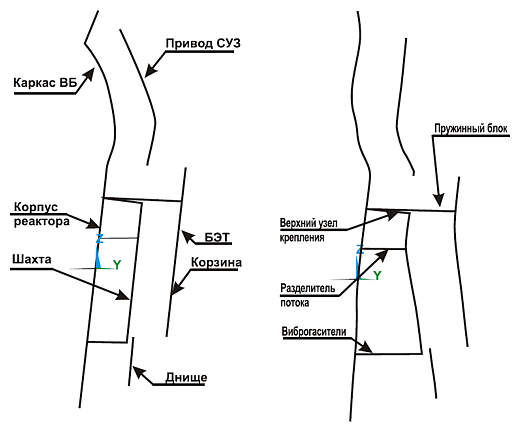 Условное отображение форм совместных колебаний шахты и Условное отображение форм совместных колебаний шахты икорпуса реактора При моделировании верхний блок разбит на каркас и приводы системы управления и защиты. Корпус реактора рассматривается совместно с крышкой. Остальные ВКУ и топливо участвуют в образовании жесткостей и масс моделируемых элементов конструкции реактора, а также в образовании связей между ними. Модель построена таким образом, что существует возможность ее рассмотрения в различных вариантах компоновки:
Для верхнего узла крепления шахты (трубчатых элементов), нижнего узла крепления шахты (виброгасителей) и разделительного кольца предусмотрена возможность задания жесткости, неравномерной по азимуту. Это становится возможным при построении для соответствующих узлов единой матрицы жесткости, получаемой суммированием матриц жесткости каждого отдельного элемента, входящего в узел. Модель позволяет вести расчет собственных частот при наличии жидкости в объеме РУ. Для этого в модель введен коэффициент, учитывающий эффект гидроупругости. Массовые доли корпуса и шахты наиболее существенны, поэтому важно проследить за совместными колебаниями именно этих элементов конструкции реактора. Из множества типов колебаний корпуса совместно с ВКУ рассматриваются две низших формы совместных колебаний шахты и корпуса:
С использованием разработанного программного продукта можно моделировать следующие аномалии:
Примеры расчетов частот и форм колебаний приведены на рисунках. 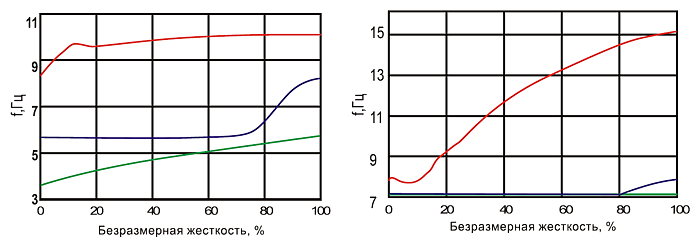 Зависимости собственной частоты колебаний шахты по модам R1 и R2 от безразмерной Зависимости собственной частоты колебаний шахты по модам R1 и R2 от безразмернойжесткости соответствующего узла 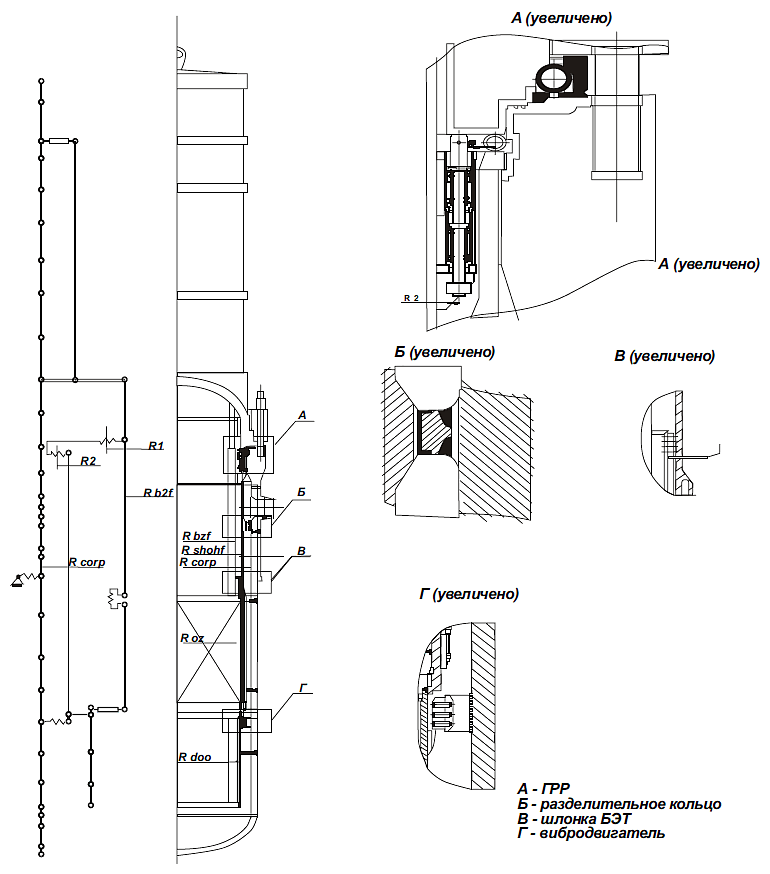 |